Print
out of http://mathematicallysane.com/analysis/mathwars.asp
![]()
What are the "Math Wars" in California All About? Reasons and Perspectives
Judith Sowder, San Diego State University
Many of you will recall the pain of learning the times tables, or the procedure for long division. But then again, some of you never experienced that pain. For you, school mathematics was easy. Think back though, and you should remember that such was not the case for many of your friends. Those who found mathematics painful then are today likely to be math anxious, unafraid to say that they did not do well in mathematics and still can't "do" fractions, whereas they would never admit to being poor readers. I can't begin to tell you how many of these people I meet on planes or at parties, people who, when they ask what I do and hear that I teach mathematics, freely tell me how bad they were in their school mathematics. For strange reasons, it is considered "OK" to be non-math literate. Unfortunately I meet many of these people in my mathematics courses for prospective elementary teachers.
Those educators and parents who feel that the traditional curriculum is inadequate for the vast majority of our students want to change the curriculum; they want to "reform" it. They advocate an emphasis on understanding mathematics, and claim that learning happens more quickly and more easily when understanding is the focus of mathematics instruction. They say that they want to produce citizens who can use mathematics, who can solve problems, who can work cooperatively on mathematics and communicate mathematically, who can "make sense" mathematically of the world around them. They claim that although computational skills remain important, these skills should not be the sole focus of the curriculum in the elementary grades. They prefer a curriculum that develops "number sense" and reasoning and problem solving skills.
On the other hand, we have a group of quite vocal citizens who fear that this new, "fuzzy" math, as they call it, will be detrimental to their children; that it lacks rigor; that children must first develop skills before they can understand concepts; that skills are best learned through memorizing procedures then practicing them until they are automatic; that allowing calculators in classrooms will make children dependent on their use. They claim that there is no research to support the changes advocated by the "reformers." Many of these people are very successful and want their children to have an equal chance at the same successes. Who can blame them for having this goal?
Unfortunately, there are extremists within both groups who have made the debate hot and acrimonious. There are those "reformist teachers" and even some curriculum developers, who, in their zeal to jump on the bandwagon of reform, become so involved in making mathematics "fun," and who treat the use of manipulatives, group work, and using realistic situations as ends rather than as means, that they lose sight of the mathematics their students need to learn. They leave the public with the false impression that the reformers believe that there should be no drill and practice, that no skills need to be automatized, that getting right answers does not matter.
There are, on the other side, reactionaries who believe that any change is bad, that because they learned mathematics the traditional way, their children and grandchildren should learn it the same way, that widespread testing on computational skills will keep us on the straight and narrow path. They are horrified when their children take out a calculator even if it is to finish off the calculations in a problem that yielded particularly messy numbers. They think that any curriculum change should be preceded by widespread testing, but not on their children, thank you anyway. Some of those who claim to be their spokespersons fill the email listserves with long, sometimes hateful and libelous accusations.
What are the real distinguishing characteristics between the two groups?
I would like, today, to put aside the rhetoric of the extremists on either side who close themselves off from considering whether or not the "other side" has any valid concerns or any valid answers. Certainly there are good and reasonable people on either side of the current debate. Even so, there are several ways to distinguish those who advocate a concept-driven reform curriculum from those who remain defenders of a skills-oriented traditional curriculum. I will discuss today the ways that I see these two sides differing: They hold different beliefs about what mathematics is, different beliefs about how mathematics is learned, different understandings of what it means to know mathematics, and different ways of interpreting what research has to tell us on these issues. In a nutshell, they represent different value systems. I believe that rational, reflective discussion and exploration of these issues can bring the two sides closer together. Thus, although the two sides may not reach total agreement, they can come to understand the issues better and find ways to compromise. I am told that California schools educate one-seventh of the students in this country. There is too much at stake to continue the fighting, to take a chance on sacrificing the mathematical education of our children by not reaching some agreement on what that education should be.
1. What is mathematics? Or at least, what do we believe it is?
The prevailing public view of mathematics
is that it is a set of rules, skills, and facts that need to be learned, maintained,
and drawn upon when necessary. Others view mathematics as a unified (but static)
body of knowledge, with all the parts logically connected, there to be discovered
by humans. Holders of both of these views tend to want a curriculum that assists
students in learning the rules. Those who want to maintain the current traditional
mathematics curriculum that is taught now in the vast majority of classrooms
feel that the curriculum ought to be carefully and logically sequenced so that
children come to learn, bit by bit, the parts of this body of knowledge appropriate
for their grade level. Mathematicians are seen to have the power to discover
new facets of mathematics, but even getting a glimpse of this power is not considered
to be within the role of school mathematics.
Yet others view mathematics as dynamic--invented
rather than discovered. When the mathematician Rueben Hersh was asked, "What
is mathematics?" he responded that "Mathematics deals with ideas.
Not pencil marks or chalk marks, not physical triangles or physical sets, but
ideas" (p. 22). He went on to say that mathematics is invented and created
by humans in response to needs of science or daily life, and that "once
created, mathematical objects have properties which are well-determined . .
. and possessed independently of our knowledge of them" (pp. 22-23). Hersh
believes that "knowing mathematics is making mathematics". My late
colleague Alba Thompson found this view of mathematics reflected in many of
the current documents that advocate reforming the curriculum.
The conception of mathematics teaching that can be gleaned from these documents is one in which students engage in purposeful activities that grow out of problem situations, requiring reasoning and creative thinking, gathering and applying information, discovering, inventing, and communicating ideas, and testing those ideas through critical reflection and argumentation. This view of mathematics teaching is in sharp contrast to alternative views in which the mastery of concepts and procedures is the ultimate goal of instruction. However, it does not deny the value and place of concepts and procedures in the mathematics curriculum. (Thompson, 1992, p. 128)
2. How do children best learn mathematics?
For several decades now there have been competing views among psychologists about how children learn. The behaviorist tradition is based on stimulus-response theory, and teaching that reflects this theory is usually quite directive. Skill learning is paramount, and skills are thought to be acquired through a process of practice of isolated skills, finally coming together to form more complex skills. Douglas Carnine, of the University of Oregon, is, for example, an advocate of direct instruction of basic skills, carefully taught so that children will not make any errors. He describes one step in learning subtraction as follows:
In preparing students for subtraction that involves borrowing, the curriculum designer can emphasize the ways in which borrowing problems are not the same as addition problems and simple subtraction problems. To highlight these differences, the designer might present a series of simple problems:
Students would be told that they had to subtract the bottom number from the top number. The students would then cross out the problems that they couldn't work and write the answers to the problems that they could work. This activity reduces the sameness between addition and subtraction by sensitizing students to the consequences of having a smaller number on top (Carnine, 1990, page 374, bold-face mine).
In the cognitivist tradition, teaching is considered to be a process of helping children organize their knowledge through making many connections and forming relationships. Knowledge is seen as a connected web in "which the linking relationships are as prominent as the discrete pieces of information" (Hiebert, 1986). Instruction on addition and subtraction in this tradition focuses on modeling many types of problems. Symbols are not introduced until children can first solve problems without symbolizing them; children then learn that symbols are just ways of representing problems. Thus, a subtraction problem, if presented in a physical situation, would preclude the type of error described by Carnine. Children would solve the problem "There were five birds in the tree, and three flew away. How many were left?" by first modeling the situation with counters or with fingers, and only then learning to represent it as 5 - 3 = ?.
In this tradition, the focus is on understanding subtraction situations, and subtraction is more difficult for young children than one might first think . For example, we would say that if there are 5 boys and 3 girls, there are 5 - 3 or 2 more boys than girls. But some children protest that we cannot take girls away from boys, and must be shown how this situation can be represented by subtraction, for example by having 5 boys and 3 girls come to the front of the classroom, and having 3 of the boys hold hands with the 3 girls. Now they can see that the number of boys holding hands can be subtracted from the total number of boys. Unfortunately, most traditional textbooks rarely get to problems beyond "take away", represented symbolically, and children are left with very limited notions of subtraction and are dependent on a memorized procedure for finding answers.
These examples of learning subtraction
should help you understand the fundamental differences between a behaviorist
approach and a cognitivist approach. The behaviorists focus on learning rules
for symbol manipulation while the cognitivists focus on using situations to
help children understand what subtraction is all about and then how it should
be represented. Do we value more the ability to solve symbolic problems disassociated
from problem situations, or do we instead value more the ability to understand
problem situations and express this understanding through symbolically representing
the problem and solution. The question of whether developing skills with symbols
leads to conceptual understanding, or whether the presence of basic understanding
should precede symbolic representation and skill practice, is one of the basic
disagreements between the behaviorist and cognitivist approaches to learning
mathematics.
3. What do we mean by "doing well" in mathematics?
We would all say that we want our children to do well, to gain expertise in mathematics. But what is expertise? Giyoo Hatano, a Japanese psychologist, distinguishes between two types of expertise. The first he calls routine expertise. A person with routine expertise can solve routine problems quickly and accurately, using automatized procedures. Such expertise is acquired when one repeatedly solves problems of the same type, for which efficiency and right answers are valued but for which understanding is not so important. This type of expertise is sufficient for many situations in which mathematics is used. It is this type of expertise, I believe, that the "anti-reform" group wishes for our students. In this country, the acquisition of routine expertise in carrying out paper-and-pencil calculations has long been an objective of schooling in mathematics, and certainly, before calculators became ubiquitous, routine expertise was a necessity. (I am reminded of a film I saw about the making of the atom bomb. Each scientist was followed around by a group of graduate students who performed all the necessary calculations for them. Routine expertise was very necessary for these graduate students.)
There is another type of expertise described by Hatano. He calls this adaptive expertise. This type of expertise requires understanding of how and why procedures work, and how these procedures can be modified to fit changing constraints of a problem. It is this adaptive expertise that those who want to reform the curriculum believe should be our goal.
Let me provide an example of a problem that can be solved routinely or adaptively:
Fred and Frank are two fitness fanatics on a run from A to B. Fred runs half the way and walks the other half. Frank runs for half the time, and walks for the other half. They both run and walk at the same speeds. Who finishes first? (Mason, Burton, & Stacey, 1985, p. 171)
When we have given this problem to prospective middle school and secondary teachers, those who are on automatic pilot tend to tackle this problem in a very routine fashion, setting up equations and finally reaching the correct answer, but without any real insight to the problem. Those who tend to approach mathematics problems adaptively first reason about what is being asked. They are more likely to say: "If Fred runs half the way and walks half the way, he is running for a shorter length of time than he is walking. But Frank is running the same amount of time he is walking, so he runs for more time than Fred does, and finishes first." This solution is based on the insight into what is happening in this problem.
Hatano suggests that there are three conditions necessary to acquire adaptive expertise.
- The first is that one must frequently encounter novel types of problems. In mathematics classes, this would mean that it is not sufficient for a teacher to present a way of carrying out a procedure, then have children practice it; students would need to sometimes develop their own procedures, because developing procedures is a skill worth having, and this skill cannot be learned unless there is first understanding. We have to accept that mistakes will be made, and that finding and correcting mistakes often leads to new insights. The right answer is important, but so is the process of finding it.
- The second condition is that one must be encouraged to seek comprehension. In mathematics classes, I would interpret this to mean that children must make sense of what they are doing, and in fact, must believe that mathematics makes sense, and seek out that sense. Lauren Resnick, a cognitive psychologist, claims that people who have been truly successful in mathematics share the belief that mathematics makes sense (1986). However, we all know that the vast majority of people do not share this belief about mathematics.
- The third condition is that one must be relatively free from pressure to obtain external reinforcement. Internal motivation is more likely to lead to adaptive expertise, but will be snuffed out by too much external pressure. Many times good problems take a long time to complete. Unfortunately, we have given our students the idea that if a problem cannot be solved in 5 minutes, it is not solvable, at least not by them.
Hatano is not alone in his thinking
about expertise. Studies of expertise in different cognitive domains have led
Dreyfus and Dreyfus (1986) to hypothesize that practice of rules does not necessarily
develop true expertise, which in fact includes many capabilities that are acquired
independently of rules.
4. What does research have to offer in the domain of school mathematics?
To consider all of the research in mathematics education would take us far beyond the limitations of this talk. Rather, I want to focus here on what research is, because our interpretations of whether or not there is research supporting change will depend on this crucial issue of what we consider research to be. There are basically two types of research carried out in mathematics education. On the one hand, quantitative, or experimental, research focuses on working with large groups, and using statistical analysis to determine cause and effect and the relative significance of differences found. This type of research is powerful, and it is hard to argue with the results if it is carefully done. Some questions can be answered only by experimental research. However, it is worth noting that it is very difficult to undertake experimental studies to compare curricula. Statistical tests depend on many assumptions, the most important being random assignment to groups being compared. But random assignment, except for brief studies, is not always possible. Seldom are children in elementary school randomly assigned to classes. Yet the validity of experimental research depends on whether the underlying assumptions have been respected, or violated. There are other factors difficult to control, such as teacher effect.
Another type of research that has become a mainstay in the study of mathematics learning is called qualitative research. Qualitative methodology is based on the assumption that understanding in the human sciences cannot be adequately approached through methodologies developed for the natural sciences. This interpretivist approach to research is based on methods used in the social and anthropological sciences, and has long been a mainstay in European studies of educational phenomena. In this research paradigm, the researcher often works with just a few students, or teachers, or classrooms, and studies them in depth, through observations, interviews, individual assessments, and the like. Qualitative research is often used as a complement to quantitative research. Thus, for example, an experimental study might tell us that the majority of fourth-grade children in a particular school district are unable to solve one-step word problems that involve multiplication and division. But a qualitative study, involving observations of individual children solving problems, or having children think aloud as they work problems, could provide us with information about why this is the case. Do the children understand what multiplication means and when a problem calls for multiplication? Or are they just unable to multiply accurately? Do they suffer from the misconception that "multiplication makes bigger and division makes smaller" so that when they multiply by numbers less than one they continue to expect an answer greater than either factor, and will divide to get such an answer even though the problem calls for multiplication?
Why is this distinction between the two types of research an important issue? The California State Board of Education recently funded a project to provide a data base of all relevant research in mathematics instruction. But the Board and the project director believed that only empirical research was valid and so all qualitative research was excluded from the data base. In the proposal the project director stated, "Through a series of steps described in the next section, we will narrow approximately 2500 citations to those that report empirical experimental studies of mathematics instruction" (A Synthesis of K-12 Mathematics Research, page 1). Thus, much of what we know about children's learning of mathematics, carried out with all the rigorous standards of qualitative research as defined by the social and anthropological sciences, was simply ignored as invalid. In other words, much of the research supporting change was simply not even on the table for consideration.
How do the two groups establish communication?
A colleague introduced me to this exchange (Menashe & Radosh, 1967, P. 150-151), which speaks volumes about what happens when two groups, or even two people, fail to share fundamental values and beliefs.
Dear Professor Rapoport:
I guess we are not getting anywhere. Your use of evidence and assumptions, inferences and innuendo, are so foreign to my own standards that I doubt if we can gain much by pursuing our correspondence further.
McGeorge BundyDear Mr. Bundy:
We agree on one point, namely, that we are not getting anywhere. I wonder, however, if some thought should not be given to our failure to establish communication. I am able to communicate with thousands of my colleagues, presumably because we have similar standards of evidence, assumptions, and inference. If by innuendo you mean the connotative use of language then we also use "innuendo" as an aid to communication. (excerpted from a longer letter)
Anatol Rapoport
Yes, some thought does need to be given to our failure to establish communication. But this communication must be based on knowledge of where the other side is coming from. It should be apparent by now that the two sides represent very different value systems. One definition I've seen for value system is ". . . a small number of values organized in a coherent framework. The values people hold are assumed to have cognitive, affective, and behavioral consequences. Values function as the 'criteria people use to select and justify actions and to evaluate people and events'" (Schwartz, 1992, p. 1, referenced in Rohan & Zanna, 1996, p. 255). I do not believe it is possible to seriously discuss the form the mathematics curriculum should take until each of us begins to try to understand the value system of "the other side."
For those of you in my audience today, I want to share with you where I am coming from. If you are on "my side" you will nod your head in agreement. If you are on "the other side", then I ask of you simply to consider what I have to say, and try with me to find common ground for discussion.
Where I come from,
and why
I am one of those who believes that traditional mathematics instruction is failing
the vast majority of our children. I believe that we need to change the way
we teach mathematics to children. I have not always remained even-handed in
my remarks thus far, so this announcement will undoubtedly not come as a surprise
to you. I entered this field because I saw, in my own teaching of mathematics
all the way from the elementary grades through university, that some students
"got it" but most did not. Something was wrong, and I wanted to be
among those who worked on fixing the problem. Several years ago I began to look
at what children knew about numbers and number operations. In a very early study
I looked at what children understood about numerical estimation. Twenty-nine
students from several different schools and school districts, from different
socioeconomic levels and representing a range of ability, were interviewed and
asked to estimate in 12 problems; some purely computational, and some in real
world situations. I'll show just two of the problems here:
1. The sum of 148.72 and 51.351 is approximately how much? How did you get your answer?
Fewer than half said that this sum is about 200. Over a third gave an answer with a decimal portion, such as these two students:
(a) "200.071. Well, the sum of 72 and 35 is about 70, plus I added 1 to the end, and then 148 and 51 is about 200."
(b) "150.470. Because 148.72 is about 100.70, and 51.351 is 50.400. Add those."
Clearly, these students understood a decimal number to have two parts, but they did not understand that a decimal number represents one quantity, not two quantities to be considered separately. The second student also had very rigid, rule-based notions about rounding.
2. 789 x 0.52 is approximately how much? How did you get your answer?
It occurred to only 5 of the 29 students to replace the 0.52 with 1/2, or .5 or 50%. Several students claimed this problem was impossible without paper and pencil, and refused to try it. The majority rounded 0.52 to 1 or even to 0 in order to estimate. Here are some sample answers:
"789. I rounded .52 up to 1 and multiplied."
"Zero. This [789] is a whole number and this [0.52] is not. It [0.52] is a number but it is very small. You round 789 to 800, times 0, is 0."
In both problems, remembered rules about rounding took precedence over applying common sense. But then, I doubt that these students even knew it was possible to make sense of these problems. The students did not have what I have come to call number sense, a term that has since grown in popularity as an indicator for understanding how numbers are used.
For the next several years, my research involved dissecting the mathematical understanding and skill needed to estimate and to compute mentally, and designing and testing intervention materials that could help students in Grades 5 through 7 develop a strong understanding of numbers and number operations. Let us take, for example, a look at mental computation. Try this problem yourselves, mentally: 25 x 16.
Here are some ways I have seen this problem worked:
5 x 5 x 4 x 4 is 5 x 4 x 5 x 4 is 20 x 20 is 400
100/4 x 16, cancel the 4s so it's 100 x 4 = 400
16 is 2 x 2 x 2 x 2, so 25 x 2=50, 50 x 2=100, 100 x 2 = 200, 200 x 2 = 400
5 x 16 = 80, 80 x 5 = 400
(20 + 5) x 16 = 20 x 16 + 5 x 16 = 320 + 80 = 400
25 x (10 + 6) = 25 x 10 + 25 x 6 = 250 + 150 = 400
"Put the 16 under the 25, take 6 x 5 is 30, write down the 0, carry the 3, then 6 x 2 is 12, add the 3, write down the 15. Then take ..." etcetera. This way rarely gives the right answer, because the child looses the way or forgets some step.
In my many interviews with children in middle school, and adults in my teacher preparation classes, I have seen the last method used far more frequently that the previous six methods. How would you prefer to have your child solve this problem? The first six ways all involve a great deal of flexibility in representing numbers in different ways: 16 as 4 x 4, or as 10 + 6, or as 2 x 2 x 2 x 2. They demonstrate a knowledge of place value, that is, recognizing that 25 is 2 tens and 5 ones. They use this knowledge to break numbers down into their component parts. They show an ability to work with multiples of 10. They demonstrate their knowledge of basic properties of operations (the last two demand understanding of the distributive property of multiplication over addition). There are many instances when the "times tables", that is, basic multiplication facts, are called upon. (I have found that students who cannot do mental computation often do not know their basic multiplication facts. This knowledge is a must and you will not find any teachers worth their salt saying that quick recall of multiplication facts is unnecessary.) I contend that the seriousness of students depending on pencil and paper to find the product of 25 and 16 is equal to that of having students dependent on a calculator to solve a simple computation problem.
In the remainder of my presentation I will not provide details of my research, but rather, I will use it as a foundation for the rest of what I have to say. And I will limit this talk to computation, a seemingly mundane topic, but one that I estimate the typical child spends some 1000 school hours learning in Grades 1 through 7, not counting time spent on homework. I would further estimate that some 240-300 of these hours are spent learning the long-division algorithm--if concentrated, this would be equivalent to two years of school mathematics. So the topic of computation is worth some discussion.
Computational operations. I'll begin with some research on arithmetic operations. My husband and I undertook a research study several years ago to come to better understand how students solve "story" problems, I interviewed a seventh grade student, whom I will call Dana. She was considered to be one of the best math students in her class. I asked this student to solve several problems for me, such as "If each box holds 32 pens, and you have 9 boxes, how many pens would you have altogether?" She was able to give me the right answer to any such problem I asked her. But each time I asked how she solved the problem, I found out that she tried all four operations: For this particular problem adding would not give a large enough number, neither would subtraction. Because 9 did not go evenly into 32, division was probably was not the way to go either. But 32 x 9 gave a number that was about the right size. In other words, she had no idea why she should multiply to get the answer! So, when I then asked her to solve some problems that required more than one operation, such as: "A carpenter has a board 200 inches long and 12 inches wide. He makes 4 identical shelves and still has a piece of board 36 inches long left over. How long is each shelf?" Dana was lost. There are four numbers in the problem, and no one operation will render a solution. There were just too many things to try, and although Data put on a heroic demonstration, she was unable to solve this problem. Dana was not alone--my husband has interviewed many elementary school children, and has written about the limited strategies the majority of them use. Rarely did a student choose an operation by making a sensible interpretation of a situation and realizing that the situaion called for that operation.
The literature abounds with examples of children who make no connection between what they do computationally, and what they do to solve problems. Here is one:
Auburn correctly solved addition tasks presented horizontally, but not vertically. That is, she said that
16 + 9 = 25, but that
The following exchange then took place:
In: So when we count we get 25 and when we do it this way (points to the worksheet) we get 15. Is that OK to get two answers or do you think there should only be one answer?
A: (Shrugs her shoulders).
In: Which one do you think is the best answer?
A: 25
In: Why?
A: I don't know.
In: If we had 16 cookies and 9 more, would we have 15 altogether?
A: No.
In: Why not?
A: Because if you counted them up together, you would get 25.
In: But is this (points to the answer of 15 on the worksheet) right sometimes or is it always wrong?
A: It's always right.
(That is, when given in vertical format the answer is always 15.) (Cobb, 1988, p. 98)
These and many other such interactions make it clear that children who learn rotely understand algorithms to be inviolable. When the answer differs from one based on common sense, such as with counting cookies, the student does not see this as problematic. Mathematics class and the real world are completely disassociated. An English friend, who was a school inspector, once asked a child why the answer found with some manipulative blocks, called bricks there, was different from an answer obtained by using the algorithm (procedure). The response from the child was "Bricks is bricks and sums is sums." They had nothing to do with one another.
Computational procedures. Children in classrooms in which sense-making is taken as a given can do wonderful things with number problems. Kamii (1994) described a third-grade classroom in which children were given the problem: "Every Christmas my father gets big boxes of fruit of various kinds, like Indian River oranges, from his company. We got so many pieces of fruit that we had to give some away. This year we ended up making 24 grocery bags of fruit with 16 pieces in each bag. How many pieces did we bag altogether?" (p. 88). Because the teacher believed that children should understand and solve problems before procedures are taught, these students were not taught the standard multiplication procedure until they could work the problems on their own. Here is how Lila did this problem:
| There were several different
procedures used. Later, if the teacher should introduce the algorithm: |
|
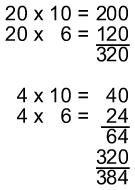
|
|
children could easily see where these numbers come from. The procedure on the left could be tightened up to introduce the standard procedure on the right (although it need not be).
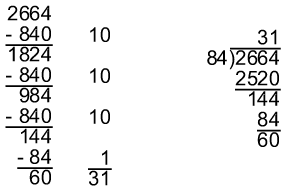
How many of you can recall learning the long division algorithm? Suppose I tell you that I can show you an easier way to do long division, albeit a way that may take slightly more time to do. (Of course, if you weigh the time spent learning the method that does not make sense to you, perhaps time favors my procedure.) Here is a situation: As parents of the new septuplets, you estimate that you need 12 diapers per baby per day, or 84 diapers per day. You have been given 2664 diapers. How many days will these diapers last? There are, of course, different ways of solving this problem, but suppose you decide you are going to solve the problem by dividing 2664 by 84. This is equivalent to asking: How many 84s are there in 2664? We know there are at least ten 84s in 2664 because ten 84s is 840. We know there are not a hundred 84s since that would be 8400, which is more than 2664. So we could begin by removing (that is, subtracting) ten 84s. We'll keep a tally on the right of the number of 84s removed. We see that we can do this again, and even again. But when we have only 144 diapers left, we cannot remove ten 84's again. We can, though remove one more 84. Finally, you have 60 diapers left, not enough for another day. Add up the tallies, and we see that the diapers will last 31 days, and we will have 60 diapers left.
If a student had recognized at the beginning that I could take out thirty 84s (2520), then one 84, the student would have the traditional algorithm but for the placement of the digits and the writing down of some extra zeros. But for most children, it takes as much time to determine that the first digit in the quotient is 3 as to subtract 840 three times.
Students can make sense of division this way. It is not quite so efficient as the standard algorithm for long division, but it is less susceptible to error simply because it is understood. Efficiency is no longer a prime consideration, because you yourselves use calculators for long-division problems when they are messy or you are in a hurry. And this procedure will be better remembered, or, if not remembered, reinvented. Contrary to what some people believe, God did NOT hand down on a tablet the standard long-division procedure we all learned. It simply is a streamlined procedure that was invented when computations had to be done quickly, such as in my example of the graduate students doing calculations for the scientists. When I have showed this alternative procedure to prospective teachers, their reaction was sometimes one of anger--anger that they had been made to suffer through the mysterious and difficult long-division algorithm when it really is all so simple to understand.
There is considerable evidence that
children may know the traditional procedure for long division, but may still
be unable to apply it or interpret the answer. The Third National Assessment
for Educational Progress (NAEP, 1983) included the problem "An army bus
holds 36 soldiers. If 1,128 soldiers are being bused to their training site,
how many buses are needed?" Only 24% of 13-year-olds were able to solve
the problem correctly. The most common error was to give an non-whole-number
answer, such as
31 1/3 buses.
Another NAEP item with poor results was this one: ABOUT how much is 8/9 + 11/12? Answer choices were 1, 2, 19, and 21. Only a quarter of 13-year-olds selected 2 as the answer; most selected 19 or 21.
I've presented some strong negative examples. What can be done to change, for example, instruction on fractions? Students must first understand the meaning of the notation we use when we represent a quantity in fractional notation. They need to understand, for example, that 4/5 can be used to express four parts of a quantity that has been separated into five equal parts. (This, by the way, is only one of several useful interpretations of 4/5.) It expresses an amount. This amount can be compared to other fractional amounts, provided we stay with the same unit; that is, the quantity that we consider to be one whole remains consistent. Students I've studied can come to think about fractions in terms of their sizes. Thus, in the problem about, 8/9 is close to 1 and 11/12 is close to 1, so the sum is close to 2. This understanding of the relative size of fractions and the ability to compare them to benchmarks, such as 1/2 and 1, turns out to be fundamental to students' understanding of the arithmetic of fractions. For example, if we combine this understanding with an understanding of operations on numbers, we can now tackle the problem: What is 1 1/2 ÷ 1/3? Yes, I know you want to jump in and use your "invert and multiply" routine, but do you remember what to invert? Do you know why that procedure yields an answer? Let's back up and consider this problem. Just as earlier, we can think of this problem as the question: How many 1/3s are in 1 1/2? Well, because there are three 1/3s in 1, there are at least that many. And in 1/2 there is another 1/3, and something left over. We might represent this problem as follows:
The drawing shows us that there are 4 1/2 one thirds in 1 1/2. With sufficient work of this kind, we begin to see that, in this case, 3/2 ÷ 1/3 is the same as 3/2 x 3 (which is 9/2, or 4 1/2). (There is admittedly some slight-of-hand here--but with more time, we could fill in the details.)
In these last few minutes I've tried to convince you that computation, the mainstay of the elementary school curriculum, can be taught in a meaningful way. Children can understand the rules they learn, they can even develop the rules themselves. Rather than being less rigorous, I am arguing for more rigor. I am arguing that children should be helped to gain an understanding of the mathematics that allows them to develop a procedure if they forget the one they learned, or to invent one in a new situation the rules don't cover. I suspect that you know by now that I am on the side of reforming the curriculum in mathematics and the manner in which mathematics is taught. I believe that children can come to experience for themselves the power of mathematics when they invent their own procedures before learning standard procedures, and I not only believe but I know children who first develop concepual understanding can learn related skills more quickly and remember them longer. I believe that we should expect children to acquire adaptive expertise in mathematics. And I claim that we have learned much from both quantitative and qualitative research on children's learning of mathematics.
In closing, I say once again that the traditional curriculum is not working. The recent reports out from the Third International Mathematics and Science Study (TIMSS) indicate just how serious the problem is. This 1995 examination, by far the largest and most comprehensive international comparison ever undertaken in education, tested a half million students at three grade levels in 41 countries. At the fourth grade we are about average in mathematics; at the eighth grade we are well below average; at the twelfth grade we are among the world's worst, outperforming only Lithuania, Cyprus, and South Africa. I consider these results to be an indictment of the way we have been teaching mathematics in this country. As long as we continue warring with one another, we will fail to make inroads into solving the problems that exist with mathematics education in this country today.
References
- Carnine, D. (1990).
New research on the brain: Implications for instruction. Phi Delta Kappan,
January.
Carpenter, T. P., & Moser, J. M. (1984). The acquisition of addition and subtraction concepts in grades one through three. Journal for Research in Mathematics Education, 16, 36-44. - Dreyfus, H. L., & Dreyfus, S. E. (1986). Mind over machine. New York: The Free Press.
- Hatano, G. (1988). Social and motivational basis for mathematical understanding. In G. B. Saxe & M. Gearhart (Eds.), Childrens' mathematics (pp. 55-70). San Francisco: Jossey-Bass.
- Hiebert, J., & Lefevre, P. (1986). Conceptual and procedural knowledge in mathematics: An introductory analysis. In J. Hiebert (Ed.) Conceptual and procedural mathematics: The case of mathematics (pp. 1-27). Hillsdale, NJ: Erlbaum.
- Hersh, R. (1986). Some proposals for revising the philosophy of mathematics. In T. Tymoczko (Ed.), New directions in the philosophy of mathematics (pp. 9-28). Boston: Birkhauser.
- Kamii, C. (1994). Young children continue to reinvent arithmetic. New York: Teachers College Press.
- Mason, J., Burton, L., & Stacey, K. (1985). Thinking mathematically. Menlo Park, CA: Addison Wesley
- Menashe, L., & Radosh, R. (Eds.). (1967). Teach-ins: U. S. A. New York, NY: Praeger.
- National Advisory Committee on Mathematical Sciences. (1975). Overview and analysis of school mathematics grades K-12. Washington, DC: Conference Board of the Mathematical Sciences.
- National Assessment of Education Progress (1983). The third national mathematics assessment: Results, trends and issues. Report No. 13-MA-01. Denver: Education Commission of the States.
- Resnick, L. B. (1986). The development of mathematical intuition. In M. Perlmutter (Ed.), Perspectives on intellectual development: The Minnesota Symposia on Child Psychology (Vol. 19, pp. 159-194). Hillsdale, NJ: Erlbaum.
- Rohan, J. J., & Zanna, M. P. (1996). Value transmission in families. In J. Olson, C. Seligman, & M. Zanna (Eds.), The psychology of values: The Ontario symposium (Vol. 8). Mahwah, New Jersey: Erlbaum.
- Schwartz, S. H. (1992). The dynamics of value systems. In M. P. Zanna (Ed.), Advances in experimental social psychology (Vol. 24, pp. 1-65). San Diego, CA: Academic Press.
- Thompson, A. G. (1992). Teachers' beliefs and conceptions: A synthesis of the research. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 127-146). New York: Macmillan.
Prepared
for the Phi Beta Kappa Invited Lecture, Spring 1998
Judith T. Sowder
Department of Mathematical and Computer Sciences, and
The Center for Research in Mathematics and Science Education
San Diego State University
Return
to Math Wars in California
www.MathematicallySane.com
Home
- Analysis - Evidence
- Resources - Links
Mission - Join Us -
Help Us - Contact Us
Technical comments or questions to [email protected].